压缩与加速-剪枝方向

huangyiming
2022-02-25 7 分钟阅读时长

Yolop与模型压缩（一）剪枝，结构化与非结构化

yolop的压缩是从算法层到框架层再到硬件层的综合，本质上是卷积在规定好的数值计算规则上的优化，市场与工程运用中的常用库与对应平台的再开发

1. 数值计算与硬件

1.1 一些基础知识

  • 有关硬件：

    • 2022年主流机都是arm7架构（对应arm cortex系处理器）主流中高端机（骁龙，麒麟，联发科，Apple）的处理器皆为多组件一体化的（cpu + gpu + isp + dsp等等），一部分有专门为高维张量tensor设计的硬件优化（即AI应用）
    • image-20220222152255237

  • 有关软件库层面：

    • 现在的手机是neon指令集（arm的单指令多数据SIMD性质指令集，针对多核应用）并配合新型的vulkan图形API

    • 为了进行压缩，了解基础线性计算代数库（basic linear algoirthm BLAS）是很重要的，最著名的有cudaBLAS，中科院的openBLAS，Eigen

    • 卷积操作，实际上对应的是通用矩阵相乘（GEMM），其转换方式为image2coloumn（im2col)，如下所示，重在

    • 软件库的层次：

      pytorch训练（起BLAS的功能）->onnx格式转换->ncnn格式转化（bin、param）->ncnn根据文件编译到android上调用vulkan（如果有显卡支持）或系统api（即armeabi7）（起BLAS的功能）

2. paper、思考与代表性复现：剪枝，结构化与非结构化（pruning，structured and unstrunctured）

只需要原权重，不需要重新训练（或者仅需要fine-tuing一两轮）

另外，剪枝与稀疏都是先要mask为0的，区别在于是否直接从结构上去掉

但是，从计算角度看，是同样的，因为0做了因子，对得到的特征图中本不改存在（多出的）维度是全0矩阵

若要保证输出相同最好一层的卷积核数不变即可

2.0 API与框架

2.0.1 有关ncnn稀疏的API

  • 在github说明中、各类博客中可以得到答案没有（具体结论是ncnn编译为调用vulkan或者直接的系统api这个过程在代码层面没有对矩阵进行稀疏计算）

  • 在源码中没有任何有关稀疏的矩阵运算, ncnn中的卷积是常规的化为了gemm（General Martix Multiplation）：

    • ncnn的初步源码阅读结果是：首先，它针对各平台都有实现相应的优化，跟yolop有关的稀疏是没有的：

      image-20220218201405186（搜索sparse只有vulkan的物理设备稀疏储存，即存张量有可能稀疏）

      image-20220218202319436常用卷积都是针对neon做的并行gemm转化

      image-20220218202535454也有汇编级优化

2.1.2 pytorch层有关稀疏（sparse）的API

  • pytorch相关稀疏API
torch.sparse_coo_tensor(indices=indices, values=values, size=[4, 4])

torch.sparse.mm() # 稀疏乘法
  • 测试结果：
    • 速度上，在电脑CPU上稀疏反而比正常慢（下图c为稀疏的）
      • image-20220128005538134
      • image-20220128005642743
    • 储存上：（对12 ， 3， 3， 3的卷积核， 每个核的每个通道的（0， 0）为1.11
      • image-20220128010638218
      • 卷积核中无法使用
    • 结论：该api无法使用，原因
  • onnx必须稠密，没有稀疏API

2.0.2 nni压缩流程

import nni
import torch
import time
from nni.compression.pytorch.utils.counter import count_flops_params
#print(myNet)
testTensor = torch.randn(1, 1, 28, 28)
flops, params, results = count_flops_params(myNet, testTensor)# myNet目标网络
print(f"Model FLOPs {flops/1e6:.2f}M, Params {params/1e6:.2f}M")
  • 网络性能测试
from nni.algorithms.compression.pytorch.pruning import LevelPruner

config_list = [{ 'sparsity': 0.8, 'op_types': ['Conv2d'] }]#剪枝目标与稀疏度
pruner = LevelPruner(myNet, config_list)
pruner.compress() #非结构剪枝，生成mask0矩阵
pruner.export_model("./lenet_masked3.pth", "./lenet_mask3.pth")#保存被mask的模型，与掩码矩阵
pruner._unwrap_model() #去掉wrapper层很重要
  • 仅根据算法得出需要剪枝部分为0的网络，此时myNet需要剪枝的部分权重为0，但是结构不变
from nni.compression.pytorch import ModelSpeedup
import time

m_speedup = ModelSpeedup(myNet, testTensor, "./lenet_mask3.pth")
m_speedup.speedup_model()#加速

  • 此步过后真正改变结构被压缩

  • 取在mnist数据集上取得98%准确率的LeNet做对照原型：

    image-20220222182142126image-20220222182409066

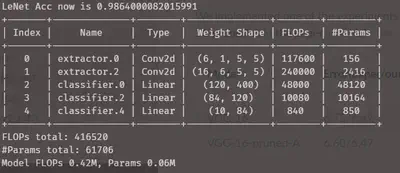
    image-20220222190328706

    可以看到张量通过一次即需40万次浮点计算

    另外，第一卷积层l1分布的情况如下（纵轴表示卷积核数量，横轴为l1范数），可见为略微接近典型情况（较少的核承担了较多的权重）

    image-20220223200639934

    第二卷积层分布如下

    image-20220223201022649

2.1 剪枝pruning方向（结构化剪枝）

  • ICLR2017 prune filters for efficient convnets， 马里兰大学1608.08710：

    • 主要讲L1剪枝，及对每个卷积核上的每一项绝对值进行求和，排序，剪枝

    • 重点在于贪心与独立两种剪枝mask的方法，贪心仅考虑核在当前卷积层中的排名，不考虑前后层间的影响，即是否将黄色部分得到的代数和算入绿色一族排名的依据

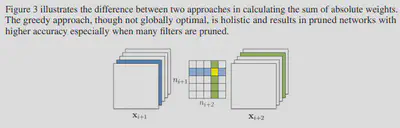
      image-20220218203701320

    • 相应的nni实现

      pruner = L1FiliterPruner(myNet, config_list)#余下同上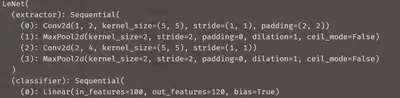

      image-20220222182727286

      可以看到卷积层与第一个全连接层参是改变

      相关参数：

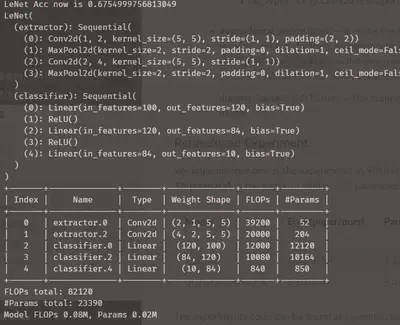
      image-20220222191053034

      可以看到浮点运算速度有5倍提升，未经重训练（fine-tuning）的准确率仅有67%，2轮fine-tuing后直接回到98%，但是按0.8的稀疏度计算是不对的，dependency_aware属性打开后结论一样

    • 阅读源码可以知道：

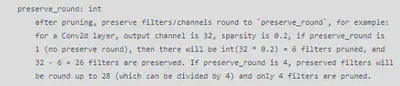
    image-20220222192341565

    ​ 剪多少是按稀疏度 * filter数再向下取整的

    ​

    image-20220222194442797
    image-20220222194532609
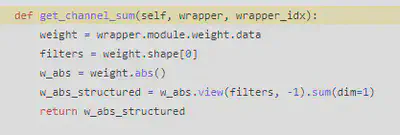
    image-20220222201407931
    image-20220222201439176

    ​ 考虑了剪后的层的对应， dependency_aware应该true，根据weight_maker的实现，在计算每个filter的L1和时没有进行前后层依 赖调整就用了topk函数排序，所以采用的是论文中的贪心算法只按当前层未被上一层影响的状态排序，nni本质是jit.trace + pytorch实现

    • L2（根据平方和排名）的nni实现，只有准确率的差别

      image-20220222202021746

  • FPGM，几何中值修剪法，arxiv：1811.0025:

    • 核心观点，按l1\l2范数filiter-level剪枝的网络，总会有所有核范数都差不多的时候，这时的剪枝必然会将有用信息剪掉，所以提出的了一种按几何中值剪枝的办法，核心idea是在要剪枝的filiter集合中不断选出当前与所有其他核们欧几里德（几何矩离）差（三维张量相减）最小的那个做为要被剪掉的核，直到满足稀疏度的数量为止
    • 因为这样说明要剪掉的核和余下其他核们共同作用的效果一样，可以被替代，故可被减去
    • 具体数学公式与算法如下：
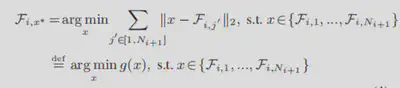
    • image-20220223191828958
    • image-20220223192039284
    • 对应的nni测试：
      • 结构、flops、参数量和l1\l2剪枝结果一样，准确率微弱高于l2，l1没区别
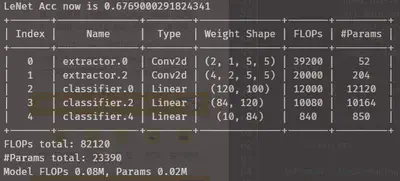
      • image-20220223194836082
    • 结论是leNet的权重分布较为接近典型情况，所以区别不大

2.2 稀疏sparse方向（非结构化剪枝）

  • MIT韩松ICLR20161510.00149：

    • 讲述了基本思路剪枝、权重公享与量化，提出这三种依次进行的three-stage的pipeline，实验结论是这三种操作不会互相影响；
    • 有关pruning的部分，韩的实现算法是选出阈值，将阈值以下的权重全部化为0，(CSR 或者 CSC）稀疏储存，这部分做到了9~13倍空间压缩， 是weight - level级的，即进入到具体核具体列具体行的每一个参数上

  • Learning both Weights and Connections for Efficient Neural Networks，韩松NIPS2015，arXiv:1506.02626：

    • 这篇和2016年的第一步过程中的prune一样，选一阈值做weight-level pruing，这个阈值是标准差乘上一个超参（工程选取的）
    • 韩松的实验环境是GTX980 + caffe + cuda，cuda有稀疏API，修改caffe底层对cuda的调用实现了稀疏加速

3 总结

  1. 正如FPGM中总结的一样，如果去weight level级剪枝，那么需要专门的BLAS去实现，正如韩松使用的应该是调了cudaAPI的caffe所以可以结构化到weight-level级的稀疏，而在我们yolop的工程链中pytorch除非在cuda显卡上，否则其稀疏乘法是很慢的，而onnx格式没有稀疏存储方式，ncnn这个起到BLAS作用的库不支持稀疏计算，所以当前weight-level级的稀疏是做不了的
  2. nni的剪枝的工程效果仅限于forward() 方法简单实现的情况，而且仅在含两层以上的全连接层才能保证输出不变，所以，对yolop而言，filiter - level的剪枝必须手写算法实现
  3. FPGM的启示和fine-tuning则说明一件事，yolop的几乎所有核在l1范数上接近（完全不是权重集中在少数通道的典型情况）不意味着pruning是无效的，有待剪枝后fine-tuning两轮的效果验证，大部分论文和实验都阐述了一个观点想学到F，网络远比你想象的小
深度学习

相关