压缩与加速-低秩分解初探

huangyiming
2022-03-11 5 分钟阅读时长

Low Rank Approximation

信息的本质是张量，张量承载着信息的值以及在整体中的坐标，而张量的运算就是两个张量的映射，映射就是规律，认识规律，即是学习，此为智能之始

核心思想：对高维张量进行近似、分解，改变卷积算法将卷积的复杂度从六阶降到近似五阶；搭配PCA or 聚类

本质上是在利用卷积核不同通道间的冗余性

卷积与矩阵

  • 将卷积操作转变成矩阵相乘的算法如下
image-20220228182832926 
  • #卷积 = unfold（实现im2col） + 矩阵乘 + fold（实现col2im)
#以下，为卷积等效替代，有padding的话会有一定的误差

import torch
from torch.nn import functional as f

inp = torch.randn(1, 3, 5, 5)
w = torch.randn(6, 3, 3, 3)
inp_unf = torch.nn.functional.unfold(inp, (3, 3)) # [2,27,6]
out_unf = inp_unf.transpose(1, 2).matmul(w.view(w.size(0), -1).t()).transpose(1, 2)
out = torch.nn.functional.fold(out_unf, output_size=(3, 3), kernel_size=(1, 1))  #[2,2,2,3]
print(out.size())
print(f.conv2d(inp, w).size())

#以下，为将以有的卷积参数进行卷积层替换

class im2colConv(nn.Module):
    def __init__(self, flts, stride, padding):
        super().__init__()
        self.ks = flts.size(2)
        self.fs = flts.size(0)
        self.sd = stride
        self.pd = padding
        self.kernelMatrix = flt1.reshape(flt1.size(0), flt1.size(1) * flt1.size(2) * flt1.size(3)).T

    def forward(self, x):
        out = nn.functional.unfold(x, kernel_size=self.ks, stride=self.sd, padding=self.pd)       
        out = torch.matmul(out.transpose(1, 2), self.kernelMatrix)
        return nn.functional.fold(out.transpose(1, 2), kernel_size=1, stride=self.sd, output_size=[(x.size(2) - self.ks + 1 + self.pd * 2) // self.sd, (x.size(2) - self.ks + 1 + self.pd * 2) // self.sd])

  • image-20220307192550732

  • retrain 之后准确率有一定的下降（5%）

    • 无法上升

  • image-20220307193859353

    • 由于是自定义层，前两层的flops根据论文计算，大约等于/4、/5左右，
    • 实际测速度：
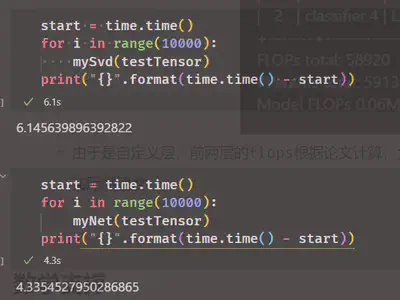
      • image-20220307195607334
      • 结果令人镇惊，目前的结论是正常的CONV后端是整体C++实现，而我自己实现的结构有重组的时间负担，可能保存为onnx模型后优势会提升

数学支撑

  • SVD奇异值分解：

    • 对任意的尺寸为m，k矩阵A， 有$ A = US \mathbf{V}^\mathrm{T} $, 其中U的尺寸为m的方阵，S为m，k的对角矩阵，V为尺寸为k的对角矩阵

    • S对角线上的值有一个特点便是值比较集中，所以可以在排序后仅对比较集中的代表性值进行计算，从而减少算量

    • 其中$ U = AA^T, V = A^TA,$ 做特征分解，遂得特征向量$u_i, v_i$而对S对角线上的奇异值可以如此计算

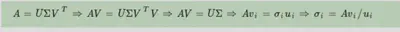
      image-20220311145052186

    • pytorch API（numpy类似）：

      u, s, v = torch.linalg.svd(a)#取得u，s，v，其中s是一维储存的，已经按值的大小排列好（u， v也对应排列好了）
torch.mm(torch.mm(u[:, :-2], torch.diag(s[:-2])), v[:-2, :])#重新计算矩阵乘法

  • 外积，cp分解：

    • $ argmin || W - \alpha ⊗ \beta ⊗ \lambda||_F$, $\alpha$, $\beta$ ,$\lambda$ 为向量（单个卷积核）对应三个一维子空间的任意向量，⊗为外积乘，再开方
    • 求法需要定义新的张量积

  • 张量的数学运算与思考：

    • 对张量求范数，结果为标量$x \in R^(I_1* I_2 * I_3 * …. *In), ||X|| = \sqrt[2]{\sum_{i_1=1}^{n}…\sum_{i_n=1}^{n} x_{i_1…i_2}^2} $

    • 张量内积, 结果为标量$x, y \in R^(I_1* I_2 * I_3 * …. *In), <x, y> = \sqrt[2]{\sum_{i_1=1}^{n}…\sum_{i_n=1}^{n} x_{i_1…i_n}}y_{i_1…i_n} $

    • 张量外积，结果为张量

      $ out_{i,j,k…} = x_iy_jz_k*…, out \in R^{IJK*….}$

    • 张量乘法有模式一积、模式二积，turker分解就是建立在其上的

    • Turker是对张量运用高阶PCA算法进行分解

    • 2D卷积是满足交换律、结合率、分配率的，

paper与最小代表性复现

  • 直接im2col + svd分解:

  • #卷积 = unfold（实现im2col） + 矩阵乘 + fold（实现col2im)
#以下，为卷积等效替代，有padding的话会有一定的误差

import torch
from torch.nn import functional as f

inp = torch.randn(1, 3, 5, 5)
w = torch.randn(6, 3, 3, 3)
inp_unf = torch.nn.functional.unfold(inp, (3, 3)) # [2,27,6]
out_unf = inp_unf.transpose(1, 2).matmul(w.view(w.size(0), -1).t()).transpose(1, 2)
out = torch.nn.functional.fold(out_unf, output_size=(3, 3), kernel_size=(1, 1))  #[2,2,2,3]
print(out.size())
print(f.conv2d(inp, w).size())

#以下，为将以有的卷积参数进行卷积层替换

class im2colConv(nn.Module):
    def __init__(self, flts, stride, padding):
        super().__init__()
        self.ks = flts.size(2)
        self.fs = flts.size(0)
        self.sd = stride
        self.pd = padding
        self.kernelMatrix = flt1.reshape(flt1.size(0), flt1.size(1) * flt1.size(2) * flt1.size(3)).T

    def forward(self, x):
        out = nn.functional.unfold(x, kernel_size=self.ks, stride=self.sd, padding=self.pd)       
        out = torch.matmul(out.transpose(1, 2), self.kernelMatrix)
        return nn.functional.fold(out.transpose(1, 2), kernel_size=1, stride=self.sd, output_size=[(x.size(2) - self.ks + 1 + self.pd * 2) // self.sd, (x.size(2) - self.ks + 1 + self.pd * 2) // self.sd])

  • image-20220307192550732

  • retrain 之后准确率有一定的下降（5%）

    • 无法上升

  • image-20220307193859353

    • 由于是自定义层，前两层的flops根据论文计算，大约等于/4、/5左右，
    • 实际测速度：
      • image-20220307195607334
      • 结果令人镇惊，目前的结论是正常的CONV后端是整体C++实现，而我自己实现的结构有重组的时间负担，可能保存为onnx模型后优势会提升

  • Exploiting linear structure within convolutional networks for efficient evaluation：

    • 本文的关点是训练好的网络往往有不同的核间往往有很多重复的地方，不如将卷积核展平后低秩分解，分解后得到的关于表达不同核重复职能的部分进行聚类

    • 这篇讲了三种将convolution layer分解的办法：

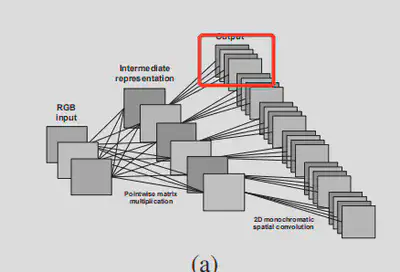
      • svd分解 + 单色卷积聚类，实际上就是将每个卷积核xy这两维展平变成一个矩阵，svd分解后，对s矩阵取rank1近似（相应的每一个u矩阵就变成了向量），然后对不同卷积核间的u进行聚类为C族，u的计算就只用计算$ F/C $次，聚类就是用对u向量每个单色中心代表所谓的单色冗余，其实就是将输出通道聚类

        image-20220310203830195

      • 双聚类然后svd分解 or 外积分解，对$ \R^{C X Y F}$的卷积核先$ \R^{C （X Y F）}$展平后三维，聚类为a类，然后这a类里每个$ \R^{（C X Y） F}展平前三维然后进行聚类，聚为b类，W就被分解成了a*b个子张量，然后对\R^{C （X Y） F`}$的每个子张量展平中间两维进行svd（三维，还是展平）分解，取rank one或者外积分解，这样以一组卷积核只负责卷积一部分输入，而且每组卷积核都被两个向量 加一个数所替代

      image-20220310203957700

    • 在lenet的复现的问题：

      • 由于原文在Eiegn3上实现，显然，聚类用sklearn的K-Means便可实现聚类, 如：

        import sklearn 
from sklearn.cluster import KMeans

flts = myNet.extractor[0].weight

flts = flts.reshape(flts.size(0), flts.size(1), flts.size(2) * flts.size(3))
us, ss, vs = torch.linalg.svd(flts)
cluster = KMeans(n_clusters=3, max_iter=5)
cluster.fit(us.reshape(us.size(0), us.size(1) * us.size(2)).detach().numpy())
print(cluster.cluster_centers_)
print(cluster.labels_)

        但显然，聚类后再送入torch.nn.functional.conv2d先进行1所输出的结果是要根据下标进行复杂的resize的，其效率之低下对小模型lenet是显然的，同时也等价于分离卷积

  • Speeding up convolutional neural networks with low rank expansions arxiv1405.3866

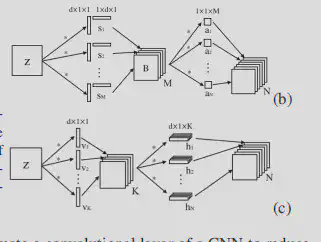
    • 提出了两种scheme，但本质是将卷积核分解后再进行空间可分离卷积
    • 区别在于用1*1恢复通道数还是第二次条状卷积改变通道数
    • image-20220311154707520

  • Accelerating very deep convolutional networks for classification and detection arxiv1505.06798

    • 同上，数学上的分解策略改变了，仍要进行空间可离卷积
深度学习

相关